Continuum (topology)

In the mathematical field of point-set topology, a continuum (plural: "continua") is a nonempty compact connected metric space, or, less frequently, a compact connected Hausdorff space. Continuum theory is the branch of topology devoted to the study of continua.

Definitions

* A continuum that contains more than one point is called nondegenerate.
* A subset ''A'' of a continuum ''X'' such that ''A'' itself is a continuum is called a subcontinuum of ''X''. A space homeomorphic to a subcontinuum of the Euclidean plane R² is called a planar continuum.
* A continuum ''X'' is homogeneous if for every two points ''x'' and ''y'' in ''X'', there exists a homeomorphism ''h'': ''X'' → ''X'' such that ''h''(''x'') = ''y''.
* A Peano continuum is a continuum that is locally connected at each point.
* An indecomposable continuum is a continuum that cannot be represented as the union of two proper subcontinua. A continuum ''X'' is hereditarily indecomposable if every subcontinuum of ''X'' is indecomposable.
* The dimension of a continuum usually means its topological dimension. A one-dimensional continuum is often called a curve.

Examples

* An arc is a space homeomorphic to the closed interval ,1 If ''h'': ,1→ ''X'' is a homeomorphism and ''h''(0) = ''p'' and ''h''(1) = ''q'' then ''p'' and ''q'' are called the endpoints of ''X''; one also says that ''X'' is an arc from ''p'' to ''q''. An arc is the simplest and most familiar type of a continuum. It is one-dimensional, arcwise connected, and locally connected.
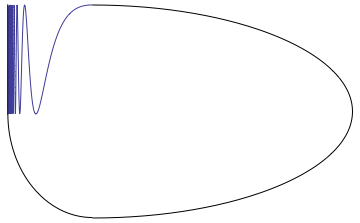
* The topologist's sine curve is a subset of the plane that is the union of the graph of the function ''f''(''x'') = sin(1/''x''), 0 < ''x'' ≤ 1 with the segment −1 ≤ ''y'' ≤ 1 of the ''y''-axis. It is a one-dimensional continuum that is not arcwise connected, and it is locally disconnected at the points along the ''y''-axis.
* The Warsaw circle is obtained by "closing up" the topologist's sine curve by an arc connecting (0,−1) and (1,sin(1)). It is a one-dimensional continuum whose homotopy groups are all trivial, but it is not a contractible space.

* An ''n''-cell is a space homeomorphic to the closed ball in the Euclidean space R^''n''. It is contractible and is the simplest example of an ''n''-dimensional continuum.
* An ''n''-sphere is a space homeomorphic to the standard n-sphere in the (''n'' + 1)-dimensional Euclidean space. It is an ''n''-dimensional homogeneous continuum that is not contractible, and therefore different from an ''n''-cell.
* The Hilbert cube is an infinite-dimensional continuum.
* Solenoids are among the simplest examples of indecomposable homogeneous continua. They are neither arcwise connected nor locally connected.
* The Sierpinski carpet, also known as the ''Sierpinski universal curve'', is a one-dimensional planar Peano continuum that contains a homeomorphic image of any one-dimensional planar continuum.
* The pseudo-arc is a homogeneous hereditarily indecomposable planar continuum.

Properties

There are two fundamental techniques for constructing continua, by means of ''nested intersections'' and ''inverse limits''.

:* If is a nested family of continua, i.e. ''X''_''n'' ⊇ ''X''_''n''+1, then their intersection is a continuum.

:* If is an inverse sequence of continua ''X''_''n'', called the coordinate spaces, together with continuous maps ''f''_''n'': ''X''_''n''+1 → ''X''_''n'', called the bonding maps, then its inverse limit is a continuum.

A finite or countable product of continua is a continuum.

See also

* Linear continuum
* Menger sponge
* Shape theory (mathematics)

References

Sources

* Sam B. Nadler, Jr, ''Continuum theory. An introduction''. Pure and Applied Mathematics, Marcel Dekker. .

External links

Open problems in continuum theory

Examples in continuum theory

Continuum Theory and Topological Dynamics
M. Barge and J. Kennedy, in Open Problems in Topology, J. van Mill and G.M. Reed (Editors) Elsevier Science Publishers B.V. (North-Holland), 1990.
Hyperspacewiki

{{Topology

de:Kontinuum (Mathematik)#Kontinua in der Topologie